Why the EU system for choosing MEPs means that small parties must collaborate for succeed
The LibDems and Green parties share an objective of getting a Peoples Vote on any Brexit proposal with a view to campaigning for the UK to remain in the EU. But they refuse to collaborate in the approaching EU elections because they are used to behaving tribally. As I demonstrate below, this is against their best interests because they must collaborate to win more seats.
Background
In the UK we usually use the First Past the Post (FPtP) system. That system is radically unfair to smaller parties and their supporters.
For EU elections the UK uses forms of proportional representation. Outside Northern Ireland we use an unfamiliar system known as the d'Hondt system named after the Belgian lawyer who described the system invented by Thomas Jefferson for the US House of Representatives.
Parties create a list of candidates for each constituency: in the EU elections these are regions. Voters vote for the party of their choice. The d'Hondt system uses a simple process to allocate seats to parties according to how many votes they receive.
The d'Hondt system is fairer than FPtP but you still need to get a fairly large percentage of the vote to get seats. As I demonstrate below, current levels of support for individual Remain parties mean that they are doomed to fail to get seats on their own, in contrast to the Brexiter parties that split the vote into larger blocks.
The D'Hont System
The European Parliament explains the system as follows.
"If there are five parties contesting five seats in one region and the votes are cast as follows:
Smartie Party: 100 votes
Jelly Baby Party: 80 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The first seat: the Smartie Party has the most votes so the first seat goes to it (the seat goes to the candidate at the top of the list of Smartie Party candidates, independent candidates being treated as a list with only one candidate on it).
The second seat: the number of votes for the Smartie Party is now divided by 2 (i.e. the number of seats the party has plus one) so the votes are now as shown below. The Jelly Baby Party now has the most votes so it gets the second seat (which goes to the person at the top of the list of Jelly Baby Party candidates).
Smartie Party now has (100 divided by 2) = 50 votes
Jelly Baby Party: 80 votes
Lollipop Party: 40 Votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The third seat: the number of votes for the Jelly Baby party is now divided by 2 (i.e. the number of seats the party now has plus one), so the votes are now as shown below. The third seat goes to the Smartie Party, which at 50 votes now has the highest number of votes. The seat goes to the second person on the Smartie Party list of candidates.
Smartie Party: 50 votes
Jelly Baby Party now has (80 divided 2) = 40 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The fourth and fifth seats: the original number of votes for the Smartie Party is now divided by 3 (i.e. the number of seats it now has plus one). So now when it comes to allocating the fourth and the fifth seat, the Jelly Baby party and the Lollipop Party both have 40 votes and will be given the fourth and fifth seats. One seat goes to the second candidate on the Jelly Baby list and the other one to the first person on Lollipop Party candidate list.
Smartie Party has (100 divided by 3) = 33 votes
Jelly Baby Party: 40 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The final result is:
Smartie Party: 2 seats
Jelly Baby Party: 2 seats
Lollipop Party: 1 seat
Kit Kat Party: 0 seats
Aero Party: 0 seats"
Background
In the UK we usually use the First Past the Post (FPtP) system. That system is radically unfair to smaller parties and their supporters.
For EU elections the UK uses forms of proportional representation. Outside Northern Ireland we use an unfamiliar system known as the d'Hondt system named after the Belgian lawyer who described the system invented by Thomas Jefferson for the US House of Representatives.
Parties create a list of candidates for each constituency: in the EU elections these are regions. Voters vote for the party of their choice. The d'Hondt system uses a simple process to allocate seats to parties according to how many votes they receive.
The d'Hondt system is fairer than FPtP but you still need to get a fairly large percentage of the vote to get seats. As I demonstrate below, current levels of support for individual Remain parties mean that they are doomed to fail to get seats on their own, in contrast to the Brexiter parties that split the vote into larger blocks.
The D'Hont System
The European Parliament explains the system as follows.
"If there are five parties contesting five seats in one region and the votes are cast as follows:
Smartie Party: 100 votes
Jelly Baby Party: 80 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The first seat: the Smartie Party has the most votes so the first seat goes to it (the seat goes to the candidate at the top of the list of Smartie Party candidates, independent candidates being treated as a list with only one candidate on it).
The second seat: the number of votes for the Smartie Party is now divided by 2 (i.e. the number of seats the party has plus one) so the votes are now as shown below. The Jelly Baby Party now has the most votes so it gets the second seat (which goes to the person at the top of the list of Jelly Baby Party candidates).
Smartie Party now has (100 divided by 2) = 50 votes
Jelly Baby Party: 80 votes
Lollipop Party: 40 Votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The third seat: the number of votes for the Jelly Baby party is now divided by 2 (i.e. the number of seats the party now has plus one), so the votes are now as shown below. The third seat goes to the Smartie Party, which at 50 votes now has the highest number of votes. The seat goes to the second person on the Smartie Party list of candidates.
Smartie Party: 50 votes
Jelly Baby Party now has (80 divided 2) = 40 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The fourth and fifth seats: the original number of votes for the Smartie Party is now divided by 3 (i.e. the number of seats it now has plus one). So now when it comes to allocating the fourth and the fifth seat, the Jelly Baby party and the Lollipop Party both have 40 votes and will be given the fourth and fifth seats. One seat goes to the second candidate on the Jelly Baby list and the other one to the first person on Lollipop Party candidate list.
Smartie Party has (100 divided by 3) = 33 votes
Jelly Baby Party: 40 votes
Lollipop Party: 40 votes
Kit Kat Party: 20 votes
Aero Party: 10 votes
The final result is:
Smartie Party: 2 seats
Jelly Baby Party: 2 seats
Lollipop Party: 1 seat
Kit Kat Party: 0 seats
Aero Party: 0 seats"
How would this work in a typical UK constituency?
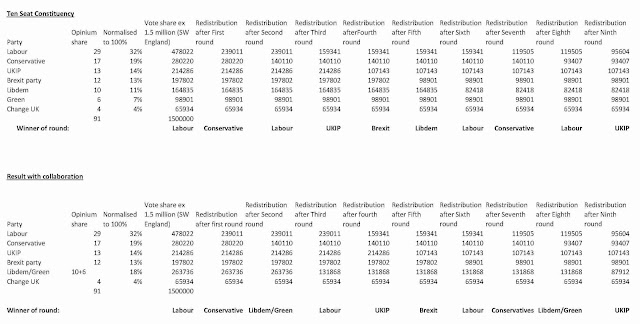
The worked example uses voter numbers from the Southwestern Constituency - 1.5 million people voted. It takes voting intentions from the Opinium poll reported in the Observer on 14 April 2019 (scroll down to find it) but excluding the SNP as this is an English constituency.
The results are as follows.
Without collaboration:
- Labour 3
- Conservative: 1
- UKIP: 1
- Brexit Party: 1
- Libdem, Green, Change UK: none
With collaboration:
- Labour 2
- Conservative: 1
- Libdem/Green Alliance: 1
- UKIP: 1
- Brexit Party: 1
- Change UK: none
Here are the workings.
This means that the Libdems and Greens should collaborate to create a shared list for each constituency. Whether a Libdem or Green is at the top of the list is a matter of sharing out the prospects of success in a way that is fair as between the parties.
This will require some negotiation. But it represents a classic win-win situation. Working together to overcome tribalism will led smaller parties to gain seats that they could never have dreamt of gaining alone. Collaboration should pay good dividends.
PS: Please see correction here: https://putneydebates.blogspot.com/2019/04/modelling-electoral-co-operation.html
PS: Please see correction here: https://putneydebates.blogspot.com/2019/04/modelling-electoral-co-operation.html
Putney Politics
Putney
15 April 2019


Comments
Post a Comment